مشتق

کاربرد مشتق در چیست؟

مفهوم مشتق در ریاضیات بیان می‌کند که یک پارامتر با چه سرعتی در زمان تغییر می‌کند. از این رو این ابزار در فیزیک کاربرد بسیاری دارد. برای مثال تصور کنید که خودرویی در حال پیمودن مسافت مشخصی است. در این حالت اگر تغییرات مسافت پیموده شده نسبت به زمان معلوم باشد، می‌توان نرخ این مسافت را در واحد زمان محاسبه کرد. از این رو در اکثر مسائلی که با سرعتِ تغییرِ یک پارامتر سروکار داریم، مشتق ظاهر خواهد شد.

مفهوم مشتق

همان‌طور که در بالا نیز اشاره شد، مشتق بیان می‌کند که یک تابع (مثلا جابجایی صورت گرفته توسط یک خودرو) با چه نرخی نسبت به متغیر وابسته‌اش تغییر می‌کند. برای نمونه در مثال خودرو، شیب تغییرات مسافت نسبت به زمان، همان مشتق است.

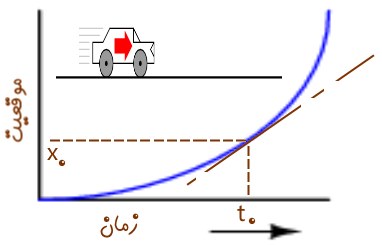
فرض کنید خودرویی فاصله مشخصی را می‌پیماید. هم‌چنین تصور کنید که نمودار مسافت پیموده شده نسبت به زمان را در اختیار داریم. شکل زیر این تغییرات را نشان می‌دهد.

این نمودار بیان می‌کند که خودرو در هر لحظه در چه مکانی قرار گرفته. بنابراین با بدست آوردن شیب این نمودار، می‌توان فهمید که در هر ثانیه این خودرو به چه میزان جابجا می‌شود. این عدد بدست آمده، همان مفهوم سرعت است.

حال تصور کنید که این تغییرات، همچون نمودار پایین غیرخطی باشند. به راستی در این حالت سرعت را چطور می‌توان بدست آورد؟

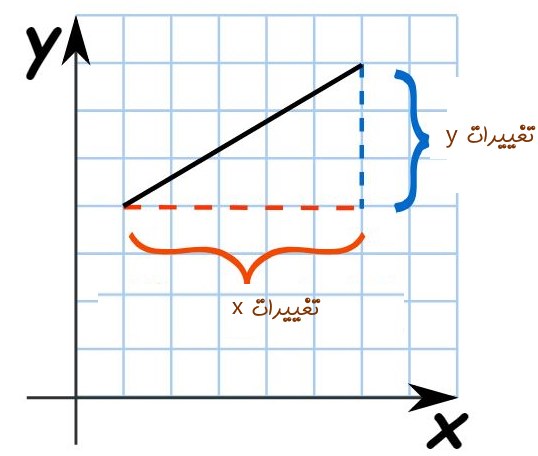
فرض کنید می‌خواهیم شیب نمودار را در نقطه (x₀,y₀) بیابیم. از این رو به نقطه دومی هم نیاز داریم. اگر این نقطه را به فاصله زیادی از (x₀,y₀) در نظر بگیریم، شیب بین این دو نقطه، عدد دقیقی را از شیب در نقطه (x₀,y₀) بدست نمی‌دهد. بنابراین بایستی چه کرد؟ حال نقطه دوم را بسیار نزدیک به (x₀,y₀) در نظر می‌گیریم. در حقیقت مختصات نقطه دوم به صورت $$(x_0+\Delta x,y_0+\Delta y)$$ در نظر گرفته شده. بنابراین شیب بین این دو نقطه برابر است با:

$$\frac{y_0+\Delta y-y_0}{x_0+\Delta x-x_0}=\frac{\Delta y}{\Delta x}$$

از این رو شیب بین دو نقطهِ (x₀,y₀) و $$(x_0+\Delta x,y_0+\Delta y)$$ برابر با $$\frac{\Delta y}{\Delta x}$$ می‌شود. اما هنوز این مقدار شیب دقیقی را در نقطه (x₀,y₀) به ما نمی‌دهد. اگر فاصله دو نقطه را به صفر نزدیک کنیم دقیقا شیب در نقطه مفروض بدست خواهد آمد. بنابراین می‌توان گفت شیب در نقطه (x₀,y₀) برابر است با:

$$\underset{\Delta x\to 0}{lim}\frac{\Delta y}{\Delta x}=\frac{dy}{dx}$$

به عبارت $$\frac{dy}{dx}$$ مشتق تابع y نسبت به x گفته می‌شود. این مقدار، تغییرات تابع y را نسبت به متغیر x در یک نقطه خاص، محاسبه می‌کند. انیمیشن زیر تغییرات شیب با نزدیک شدن به نقطه (x₀,y₀) را نشان می‌دهد.

به عملیاتی که در بالا انجام شد، مشتق‌گیری تابع y نسبت به x گفته می‌شود.

بنابراین مشتق تابع (y=f(x نسبت به x برابر است با:

$$f^{\prime }\left(x\right)=\underset{\Delta x\to 0}{lim}\frac{f(x+\Delta x)-f\left(x\right)}{\Delta x}=\frac{dy}{dx}\ast$$

در توابع مختلف حاصل این حد حساب شده است.

محاسبه مشتق در توابع مختلف

در این قسمت می‌خواهیم مشتق چند تابع را بدست آوریم. البته توجه داشته باشید که مواردی که تابع y مستقیما، به‌صورت صریح بر حسب x بیان نمی‌شود، می‌توان از مشتق‌گیری ضمنی استفاده کرد.

مثال ۱

مشتق تابع f(x)=x را بدست آورید.

با جایگذاری تابع f در معادله * داریم:

$$f^{\prime }\left(x\right)=\underset{\Delta x\to 0}{lim}\frac{f(x+\Delta x)-f\left(x\right)}{\Delta x}=\frac{x+\Delta x-x}{\Delta x}=1$$

با توجه به پاسخ بدست آمده شیب این تابع در تمامی نقاطش برابر با ۱ است.

دیگر توابع

فرض کنید در جلسه امتحان حضور دارید و می‌خواهید مشتق تابع $$f\left(x\right)=xtan\left(x\right)$$ را محاسبه کنید. در ابتدا به نظر می‌رسد بایستی برای قبول شدن در این درس تا سال بعد صبر کنید! اما واقعیت این است که مشتق توابع مختلف را می‌توان با استفاده از قوانین حاکم بر آن‌ها پیدا کرد و همواره نیاز نیست تا از طریق معادله * عمل کرد. در جدول زیر حاصل مشتقِ معروف‌ترین توابع موجود در ریاضیات بیان شده است.

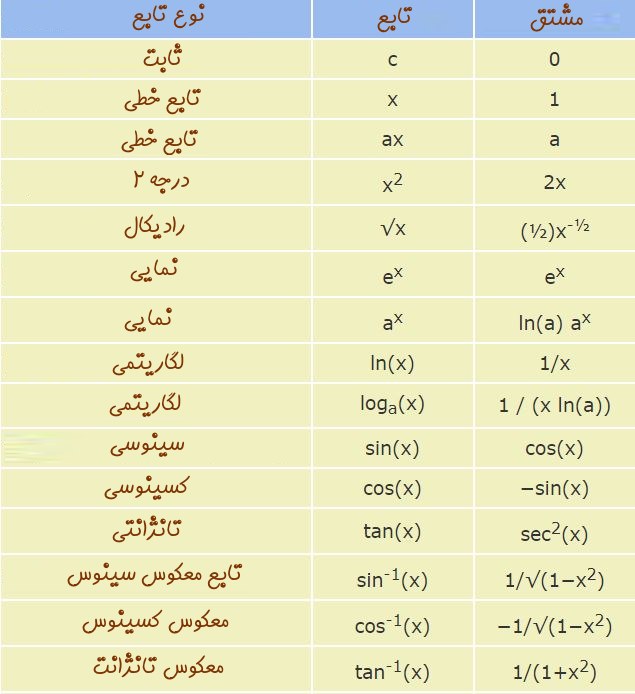
قوانین مشتق‌گیری

با استفاده از مشتقات توابع معرفی شده در بالا می‌توان مشتق هر نوع تابعی را بدست آورد. البته بایستی قوانین حاکم بر مشتق را دانست. برای مثال مشتق تابع $$y=f\left(x\right)+g\left(x\right)$$ با مشتق $$y=g\left(x\right)+y\left(x\right)$$ برابر است. در جدول زیر مهم‌ترین قوانین کاربردی در فرآیند مشتق‌گیری معرفی شده‌اند.

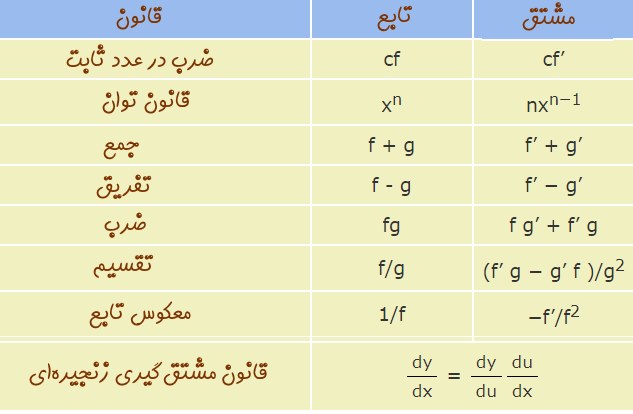
در بخش آینده با کاربرد این قوانین در محاسبه مشتق‌ توابع مختلف آشنا خواهید شد.