ضرب ماتریس‌ها

ماتریس، آرایش منظمی از اعداد است که در جدولی از سطرها و ستون‌ها آرایش یافته‌اند. در این مطلب قصد داریم تا اصول ضرب دو ماتریس را بیان کنیم. البته در مواردی می‌توان از ویژگی‌های یک ماتریس همچون ترانهاده در ضرب ماتریس‌ها بهره برد. اگر می‌خواهید اطلاعات بیشتری در مورد ماتریس‌ها کسب کنید می‌توانید به نوشته  «ماتریس ها — به زبان ساده» مراجعه کنید. در تصویر زیر یک ماتریس با دو سطر و سه ستون را می بینید:

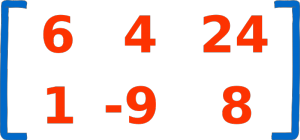
اینک می‌خواهیم عددی را در این ماتریس ضرب کنیم. باید بدانید که ضرب عدد منفرد در یک ماتریس کار آسانی است. برای انجام این کار مافی است آن عدد را در تک تک درایه‌های ماتریس ضرب کنیم و با نتایج حاصل یک ماتریس جدید تشکیل دهیم. برای مثال در تصویر زیر می بینید که چگونه با ضرب عدد 2 در درایه اول، عدد 8 برای درایه اول ماتریس حاضلضرب به دست آمده است:

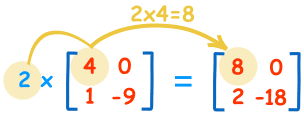
:محاسبات ضرب همه درای‌ های ماتریس به صورت زیر است

2 × 4 = 8               2 × 0 = 0
2 × 1 = 2               2 × -9 = -18

به عددی که در یک ماتریس ضرب می‌شود، «اسکالر» (scalar) گفته می‌شود. برای مثال در تصویر فوق عدد 2 اسکالر بوده است. به ضرب عدد اسکالر در یک ماتریس نیز ضرب اسکالر گفته می شود. در مقابل این نوع ضرب، مفهوم «ضرب داخلی» یا ضرب درونی (dot Product) قرار دارد که در ادامه آن را بیشتر توضیح می‌دهیم.

ضرب یک ماتریس در ماتریس دیگر

اما برای ضرب یک ماتریس در ماتریسی دیگر، باید ضرب داخلی یا  نقطه‌ای سطرها و ستون‌ها را پیدا کنیم. شاید از خود بپرسید ضرب داخلی چگونه است و چه تفاوتی با ضرب معمولی دارد. در ضرب داخلی به جای ضرب اعداد، سطر‌ها و ستون‌ها در هم ضرب می شوند. با یک مثال به توضیح آن می پردازیم:

در مثال ماتریس زیر برای یافتن جواب ضرب داخلی سطر اول و ستون اول به صورت زیر عمل می‌کنیم:

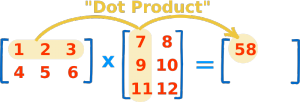
در ضرب داخلی، درایه‌های سطر و ستون های مرتبط را در ماتریس های مختلف در هم ضرب می کنیم و سپس پاسخ‌های به دست آمده را باهم جمع می‌زنیم. در مثال فوق محاسبات به صورت زیر است::

( 1, 2, 3 ) • ( 7, 9, 11 ) = 1×7 + 2×9 + 3×11 = 58

دو عضو اول سطر و ستون مربوط به ماتریس‌های اول دو دوم را با هم تطبیق می دهیم (1 و 7) و آن‌ها را در هم ضرب می کنیم. سپس همین کار را برای عضو‌های دوم (2 و 9) و سوم (3 و 11) انجام می دهیم، و در نهایت همه پاسخ‌ها را با هم جمع می‌زنیم.

اگر می‌خواهید مثال دیگری را ببینید، در تصویر زیر همین کار را برای سطر اول از ماتریس اول و ستون دوم ماتریس دوم انجام داده‌ایم:

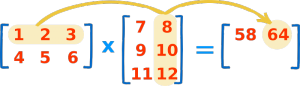
( 1, 2, 3 ) • ( 8, 10, 12 ) = 1×8 + 2×10 + 3×12 = 64

همین عمل را برای سطر دوم و ستون اول انجام می دهیم:

( 4, 5, 6 ) • ( 7, 9, 11 ) = 4×7 + 5×9 + 6×11 = 139

و همچنین برای سطر دوم و ستون دوم:

( 4, 5, 6 ) • ( 8, 10, 12 ) = 4×8 + 5×10 + 6×12 = 154

و در نهایت ماتریس زیر به دست می آید:

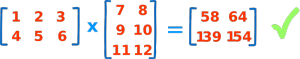
اینک کار ضرب دو ماتریس پایان یافته است.

چرا ضرب داخلی به این شکل انجام می‌گیرد؟

گرچه در نگاه نخست ممکن است این نوع ضرب کردن، روشی غیر عادی و پیچیده به نظر بیاید؛ اما عمل ضرب داخلی در محاسبه‌های مختلف امری مهم و ضروری محسوب می‌شود. در ادامه مثالی کاربردی ارائه می‌کنیم تا با دلیل این که چرا ماتریس ها را این گونه در هم ضرب می کنیم، بهتر آشنا شوید.

مثال: تصور کنید یک رستوران در طی روزهای مختلف هفته، غذاهای متفاوتی را در تعداد گوناگون به فروش می‌رساند. فهرست قیمت غذاهای این رستوران چیزی شبیه زیر است:

• کباب به قیمت سه دلار
• مرغ به قیمت چهار دلار
• غذای سبزیجات به قیمت دو دلار

و جدول زیر، تعداد فروش هرکدام از غذاها در 4 روز است:

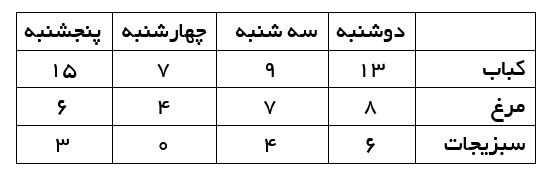
خب، اکنون می‌دانیم که درآمد فروش برای روز دوشنبه اینگونه محاسبه می‌شود:

مجموع فروش = قیمت مجموع فروش کباب + قیمت مجموع فروش مرغ + قیمت مجموع فروش غذای سبزیجات

3$ × 13 + 4$ × 8 + 2$ × 6 = 83$

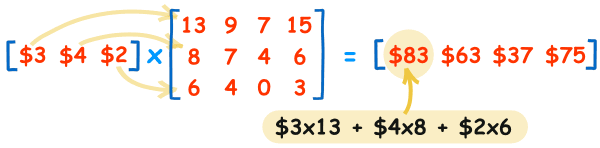
خب، این در واقع «ضرب داخلی» قیمت‌ها در تعداد فروش هر کدام از آنها است. به عبارت دیگر:

( 3$ , 4$ , 2$ ) • ( 13 , 8 , 6 ) = 3$×13 + 4$×8 + 2$×6 = 83$

ما قیمت و تعداد فروش را باهم تطبیق می دهیم، هرکدام را ضرب می کنیم، سپس نتایج را باهم جمع می کنیم.

به عبارت دیگر:

•  فروش برای روز دوشنبه از این قرار بود: کباب: 3$ × 13 = 39$، مرغ: 4$ × 8 = 32$ و غذای سبزیجات: 2$ × 6 = 12. که مجموع آنها می‌شود:

39$ + 32$ + 12$ = 83$.

•  و برای روز سه شنبه:

3$ × 9 + 4$ × 7 + 2$ × 4 = 63$

•  و برای روز چهارشنبه:

3$ × 7 + 4$ × 4 + 2$ × 0 = 37$

•  و برای روز پنجشنبه:

3$ × 15 + 4$ × 6 + 2$ × 3 = 75$

پس، تطبیق قیمت هر محصول با تعدادش مهم است. احتمالاً اکنون می دانید که چرا ما از “ضرب داخلی” استفاده می کنیم و با اهمیت آن در این گونه محاسبات بیشتر آشنا شدید. در تصویر زیر فرم کلی ضرب داخلی ماتریس‌های تعداد فروش و قیمت غذاها ارائه شده است:

بدین ترتیب می‌بینیم که صاحب رستوران در روز دوشنبه به مقدار 83$، در روز سه‌شنبه به میزان 63$ و … فروش داشته است.

سطرها و ستون‌ها

برای نشان دادن تعداد سطر‌ها و ستون‌های یک ماتریس، معمولا آن را به شکل (ستون‌ها × سطرها) می نویسیم.

مثال: ماتریس 3×2 (دو سطر و سه ستون) به شکل زیر است:

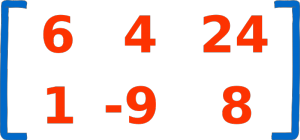
هنگامی که ضرب داخلی را روی دو ماتریس انجام می‌دهیم باید در دو ماتریس شرایط خاصی وجود داشته باشد تا بتوانیم این نوع ضرب را انجام دهیم:

• تعداد ستون های ماتریس اول باید با تعداد سطرهای ماتریس دوم برابر باشد.
• و سطرهای ماتریس حاضلضرب به تعداد سطرهای ماتریس اول و ستون‌های آن نیز به تعداد ستون های ماتریس دوم سطر خواهد بود.

مثال:

در این مثال ما یک ماتریس 3×1 را در یک ماتریس 4×3 ضرب کردیم (دقت کنید که 3 ها برابرند)، و نتیجه یک ماتریس 4×1 بود.

به طور کلی:

برای ضرب یک ماتریس m×n در یک ماتریس n×p، تعداد nها باید باهم برابر باشند و نتیجه ضرب، یک ماتریس m×p خواهد بود.

ترتیب در ضرب ماتریس‌ها

در ضرب معمولی با قانون زیر که قانون جابجایی نام دارد، آشنا هستیم:

3 × 5 = 5 × 3

اما این قانون عموما برای ماتریس ها صدق نمی‌کند چون ضرب ماتریس ها خاصیت جابجایی ندارد، یعنی:

AB ≠ BA

هنگامی که ما جای ماتریس ها را در ضرب عوض می کنیم، پاسخ معمولاً متفاوت است.

مثال:

مشاهده کنید که تغییر ترتیب ماتریس‌ها، چگونه باعث تغییر یافتن نتیجه می‌شود:

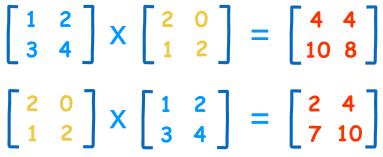
اما در یک حالت این تغییر ترتیب باعث ایجاد تغییر در نتیجه حاصلضرب داخلی ماتریس‌ها نمی شود و آن زمانی است که یکی از ماتریس‌ها ماتریس همانی (یا یکّه) باشد.

ماتریس همانی

«ماتریس همانی» یا ماتریس یکّه (Identity Matrix)، ماتریسی است که همه درایه‌های روی قطر اصلی آن برابر با عدد 1 هستند:

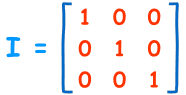
یک ماتریس همانی 3×3

ماتریس همانی خصوصیاتی به شرح زیر دارد:

• این ماتریس «مربع» است (تعداد سطرها و ستون‌هایش برابر است)،
• بر روی قطر ماتریس همانی تنها عدد 1 و در بقیه نقاط عدد 0 وجود دارد،
•  نماد این ماتریس، حرف بزرگ انگلیسی I است.

مانریس همانی، ماتریس ویژه‌ای است، چرا که هر ماتریس دیگری را در آن ضرب کنیم، پاسخ همان ماتریس اولیه خواهد بود:

A × I = A

I × A = A